Fibonacci - Golden Ratio

A Design Theory by Matthew Bates
Biography of Matthew Holden Bates
Math was not my favorite subject in high school. I do remember that one time we studied about a series of numbers. I loved that class and wished that math would be all about series, instead of x and y. A series of numbers that have a meaning seemed like something that math could be good for. Lucky for me I went to art college and didn't have to take any more mathematics, and I thought that that was it for me and math, simple, I am an artist, and math does not apply to me. It turns out I was wrong.
Art and math are connected, mostly because math is the blueprint of reality, and art is the representation of reality. Both help us to define our world. Artists use math even if they don't want to. Before I start a painting, I have to think about its dimensions. Most paintings are rectangular, with a width and a height. See, we are using math already and we have not even started to paint!
The real question is, which width and height should we use to make a painting? This is a question I ask myself over and over again, because the entire artwork will be contained inside this rectangle. How will the rectangle influence the artwork? Each artwork is a window, a window into the soul of the artist. Each painting has a meaning, it becomes iconic, and takes on a life of its own, especially when other people start to look at it in a public setting. Therefore it is crucial that the artist understands which rectangle they should use for their painting.
The freshly stretched canvas is white and pristine, its only obvious dimension is its two dimensional rectangle. This will change, by painting the canvas, the subject will come to life, and add a third dimension into the rectangle. This is the magic of art, the artist transmits something into the canvas, and we see something that was not there before. This means that the artist should understand the basic fundamentals of reality before they attempt to add dimension into the canvas. Now we are going to go back to math.
In my humble attempt to understand the world around me, I came upon a theory which seemed improbable, yet very elegant. It is the theory that the entire universe is based upon a mathematical series, which is known as the Fibonacci Series, or the Golden Ratio.
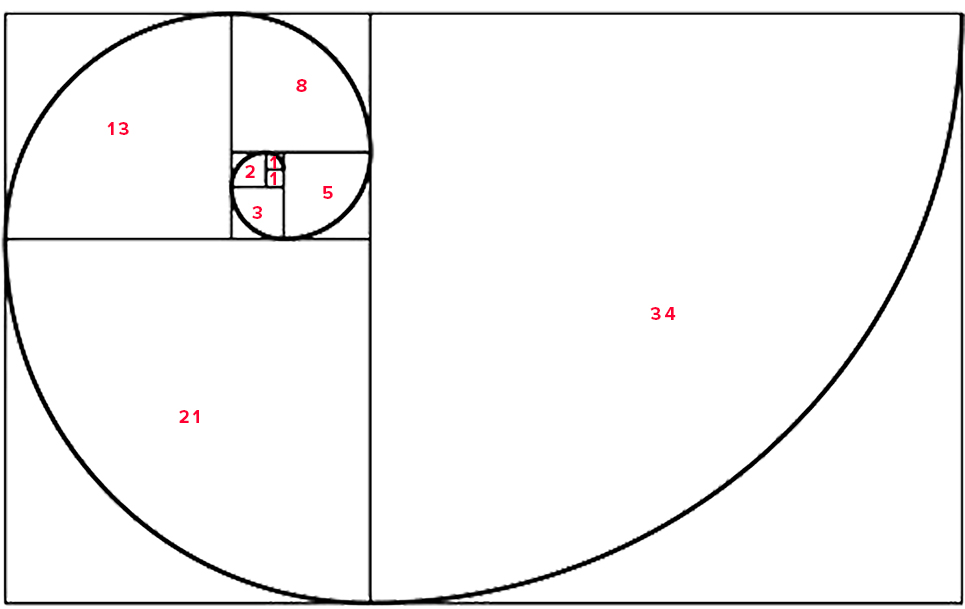
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987.....................................
It starts with nothing, a zero, and then magically it adds one, making a 100% increase into the amount of things that there are. Since there is only one, to get more, you need to add another magical one to increase the amount, now we have two. This is the part of the sequence that has always intrigued me, mostly because it is so far away from the rest of the series, zero, ones and two, not much to play with. Now that we have one and two, it is only natural to add them together to get three. Two and three are much more interesting, especially to the artist who is looking to put a rectangle together to make a painting. So three plus two, is five, and five plus three is eight, and so on into infinity, and so what? Well the what is so elegant that it defies rational thought. Take any two numbers in the series, as long as they are next to one another, and divide them together. For example let's take 610 divided by 987, the answer is .618034448............. an irrational number, like pi. What is astonishing is that if you take the next number in the series, 1597 and divide it by 987 you get 1.618034448............so it does not matter which way you divide the numbers, either the first number divided by the second or vice versa, you always get the same incredible answer, with a one or a zero in front of the ratio.
It turns out that complex systems tend to migrate eventually into the golden ratio. In plant life it is seen by the way plants grow their leaves and branches. Perhaps this is the easiest way for a plant to effectively grow, a way for the leaves to get the maximum amount of sunlight. That sounds very scientific, but I think it has a deeper seed. I could go on and on about how many examples in nature there are of this pattern, from sunflowers to nautilus shells, to the shape of distant galaxies, There is ample information on the Internet about these properties, so I won't bore you to death by listing them, if you are new to this subject just Google it, I would like to talk about something else.
I would like to posit that the Golden Ratio is a pure form of design. I have found that it can be used to get a clear image, which is beautiful to look at, therefore worthy of my time as an artist. This is based upon a lifetime of trial and error. How do I use the Golden Ratio in my designs? Simple, I use Fibonacci numbers in the rectangle of my painting. Now, you don't have to be rigid about this, there might be a combination of rectangles inside the canvas, all offering new ways to use the Fibonacci series. By using the Fibonacci numbers in the rectangular design of the painting I am placing the artwork inside of the Golden Ratio.
To show you how the Golden Ratio works, I have prepared a grid which creates the Golden Spiral. By placing each number of the Fibonacci series inside a square box which has its own dimensions, you can create the golden spiral. The next numbered box is based upon the sum of the two smaller boxes next to it and it grows exponentially. Here is that grid:
Here are some examples of paintings I have made with the Fibonacci "grid" shown on top of the finished painting:
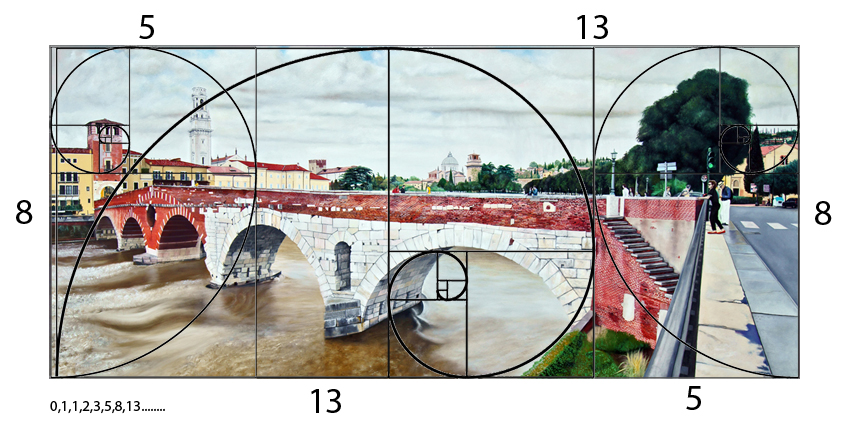
"Lovers Bridge in Verona" has dimensions which are 180cm x 80cm. By breaking up the width into two parts we get 50cm + 130cm with the height being 80cm, we get three consecutive Fibonacci numbers, 5, 8, 13. By doing this the overall design of the bridge fits naturally into the famous Fibonacci spiral. We also get two Fibonacci rectangles on the sides of the painting and a perfect square of 80cm x 80cm in the middle between the two Fibonacci rectangles.

"Entering the Duomo" shows the use of multiple Fibonacci grids in one painting.
"Piazza Santo Spirito" has the same dimensions as the painting on the right and offers a different point of view.

"Yellow Iris" uses the Fibonacci grid in its outside dimensions
"Via del Corso" has the Fibonacci Grid in its outside dimensions and shows the individual numbered squares going back into a 3d representation of the grid.
I live in Firenze, Italy, I have been here for over twenty years, Firenze is beautiful, and it offers me an infinite amount of inspiration. Whenever I leave Firenze, something happens, the inspirational juices don't flow very well, I have to look very hard to find subjects worthy of my time, and sometimes I don't find anything at all, and I have to wait to get back to Firenze to get my mojo back. This has always made me wonder, is there something special about Firenze that is different than other places? Well obviously there is a ton of history and the artwork is unbelievable, and 500 years later, we are still left in awe by what the historic Florentines have left us. But is there more? I have stared many times at the satellite image of Firenze provided by Google Maps, and it must be said that it is an amazing sight.

Beautiful Firenze seen from above.
The city has its origins in Roman times, the first outpost was supposedly made within the confines of what is now the very rectangular, Piazza della Repubblica. I thought to myself, what if I place the Fibonacci grid on top of the city, using Piazza della Repubblica as the “Number One” in the series. Something remarkable happened. The grid fits! Firenze itself corresponds to the Golden Ratio. Was it designed that way? I don't think so, it would be too hard to do, so that leaves us with the idea that Firenze has transformed itself over the centuries in a natural way to align up into the Fibonacci series.

By placing the Fibonacci Grid over Firenze, using Piazza della Repubblica as a starting place, the grid fits.
Is that why I and many others find such divine inspiration in Firenze? Does living inside of the Golden Ratio actually energize us to be able to create better art? I believe so. Just like when I place my designs inside the Golden Ratio, when I place myself inside this same ratio, the magic happens. This pure form, the Golden Ratio, may be the answer to finding peace and harmony in our lives. It has offered me a very useful tool for making art, and it has made it easier for me to find inspiration as well.
Firenze, Matthew Holden Bates
![]()
©2015, Matthew Holden Bates, Firenze, All Rights Reserved
Official Website of Matthew Holden Bates
www.mattbates.net